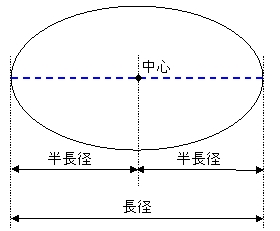
「惑星の軌道周期の2乗は、軌道の準長軸の3乗に比例します」これがケプラーの第3法則です。つまり、各惑星の「年」を二乗し、それを太陽までの距離の3乗で割ると、すべての惑星で同じ数になります。
(他の2つは「各惑星の軌道は太陽に焦点を合わせた楕円」であり、「惑星と太陽の間の線は等しい時間に等しい領域を掃引する」です。)
コペルニクス、ケプラー、およびニュートンは、太陽(および惑星)が地球の周りを移動したという考え(数千年前)に1〜2〜3ノックアウトの一撃を与えました。コペルニクスは太陽を中心に置き、ケプラーはコペルニクスの円運動を修正し(そして実際の運動の簡単で定量的な説明を提供し)、ニュートンはそれがどのように機能したか(重力)を説明しました。
ケプラーは、惑星(当時は水星、金星、火星、木星、土星)、特に火星の位置の観察の詳細な記録から、ティコブラーエによって綿密に編集された3つの法則を作成しました。
ケプラーの第3法則(実際には3つすべて)は、太陽系の惑星だけでなく、すべての惑星の衛星、準惑星、小惑星、地球を周回する衛星などにも適用されます。二次体-惑星など-が一次体(太陽など)のかなりの部分の質量を持っている場合、法律には小さな微調整が必要です。
ケプラーの法則が彼の普遍的な重力の法則からどのように導き出されるかを示すことにより、ニュートンは天と地を統一しました。おそらく科学における最大の革命です(ダーウィンの革命はもっと大きいかもしれません)。ニュートンの前は、天は地球上のものを統治するものとはまったく異なる規則に従って機能すると考えられていました。
NASAのImagine the Universe!にはケプラーの法則がきちんと示されています。このPDFファイル(テネシー大学ノックスビル大学の数学科から)は、ニュートンの万有引力の法則からケプラーの法則を簡単に導き出します。
スペースマガジンの記事と詳細:ケプラーの法則、レッツスタディ法:ケプラーはとても誇りに思う、そしてハッピーバースデーヨハネスケプラー。
天文学のキャストエピソードである重力は、宇宙の中心はどこにあるのかと同様に、ケプラーの第三法則についても説明しています。