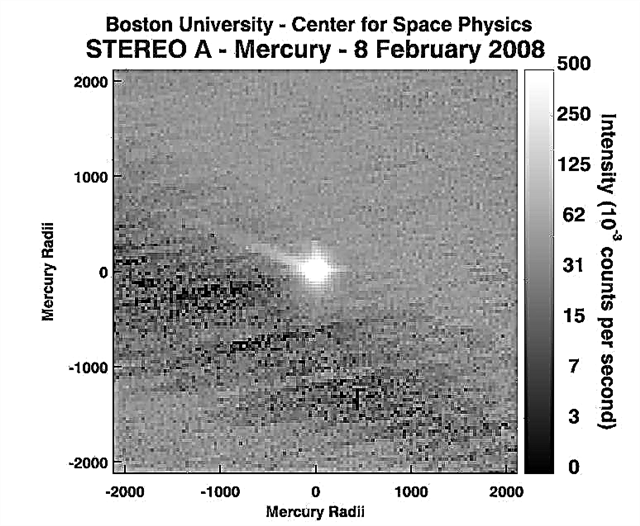
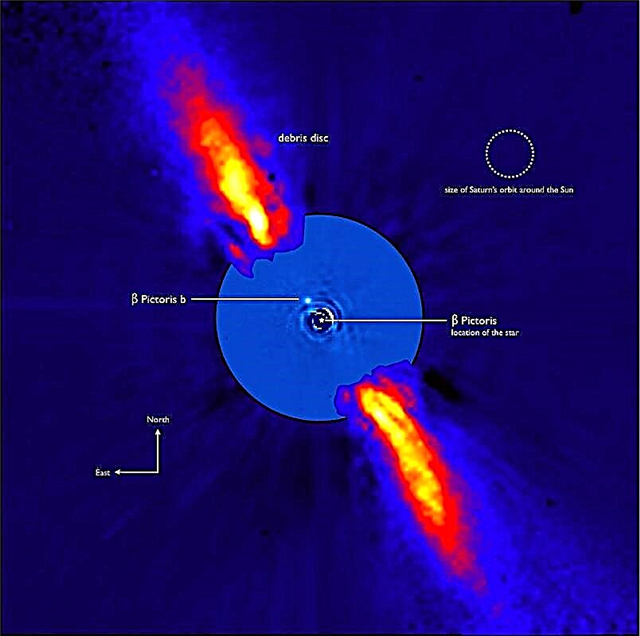
キャプション:近地点および遠地点での月の表示
私は教師として、生徒に適した簡単な設定のラボを常に探しています。私の現在のお気に入りは、チョコレートで光の速さを見つけることです。
最近arXivにアップロードされた新しい論文で、テキサスA&MのKevin Krisciunasは、メータースティック、段ボール、および曲線をフィッティングするプログラム変光星。
この方法は、偏心がオブジェクトの平均角度サイズとその振幅の半分の比率から決定できるという事実を利用しています。したがって、主な目的は、これら2つの量を測定することです。
これを行うためのケビンの戦略は、メータースティックに沿ってスライドできる段ボールの目視穴を利用することです。月の穴をのぞき、穴の角の大きさが月とちょうど重なるまでカードを前後にスライドさせます。そこから、穴の直径をメータースティックの下の距離で割ると、小さな角度の式(?= d / Dの場合、ラジアン(D >> dの場合))により角度のサイズがわかります。
穴のサイズが月と一致するまでカードを前方にスライドさせたときに、誤判定の系統的エラーを防ぐために、反対方向からもカードに近づくことをお勧めします。メータースティックの遠端から入ります。これはエラーを減らすのに役立つはずであり、ケビンの試みでは、そうするとき、彼は通常±4mmの広がりを持っていることがわかりました。
この時点で、考慮しなければならないさらに別の系統的誤差があります。瞳孔には、照準の穴に匹敵する有限のサイズがあります。これにより、実際の角度サイズが過小評価されます。そのため、補正係数が必要です。
この補正係数を導き出すために、ケビンは91ミリのディスクを10メートルの距離に配置しました(これにより、その距離から見たときに月と同じ角度サイズのディスクが生成されます)。最高のマッチを生み出すために、照準用の穴がある段ボールのスリップ すべき メータースティック上で681.3 mmに配置する必要がありますが、瞳孔の系統誤差により、Kevinは821 mmに配置する必要があることを発見しました。観察された配置と適切な配置の比率は、ケビンが使用した補正係数(1.205)を提供しました。これは、個人ごとに調整する必要があり、瞳孔の直径にも影響するため、観察時の光量にも依存します。ただし、単一の補正係数を採用すると、満足のいく結果が得られます。
これにより、必要な量(平均角度サイズと振幅の1/2)を決定するために使用できる適切に取得されたデータが可能になります。これらを決定するために、KevinはPERDETと呼ばれるプログラムを使用しました。これは、正弦曲線を可変星の振動に合わせるために設計されています。そのような曲線を?2 この目的には、フィットまたはフーリエ解析が適しています。
そのようなプログラムから、平均角度サイズと半分の振幅が決定されると、それらの比率が偏心を提供します。ケビンの実験では、彼は0.039±0.006の値を見つけました。さらに、彼が近地点から近地点までを決定した期間は27.24±0.29日であり、これは許容値27.55日と非常によく一致しています。