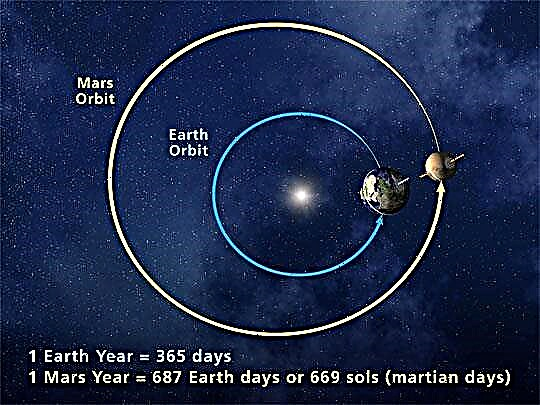
宇宙に関して言えば、偏心という言葉はほとんど常に軌道の偏心、または惑星、星、月などの天体の軌道の偏心を指します。このような軌道は形状がほぼ楕円形であり、楕円を記述する重要なパラメーターはその偏心です。
簡単に言えば、円軌道の離心率はゼロであり、放物線または放射状軌道の離心率は1です(軌道が双曲線の場合、その離心率は1より大きい)。もちろん、離心率が1以上の場合、「軌道」は少し間違っています。
複数の惑星を持つ惑星系(または複数の月を持つ惑星、または連星以外の多星系)では、各惑星は他のすべての惑星に引力を持っているため、軌道はほぼ楕円形になります。これらの加速は非楕円軌道を生成します。そして、一般相対性理論が重力を記述すると仮定して軌道をモデル化すると、軌道はほぼ楕円形になります(これはバイナリパルサーの場合は特にそうです)。
それにもかかわらず、軌道はほぼ常に楕円として要約され、離心率は主要な軌道パラメータの1つです。どうして?これは非常に便利であり、楕円からの偏差は小さな摂動で簡単に説明できるためです。
ニュートン重力下の2体システムでの離心率の式は比較的簡単に記述できますが、残念ながら、このWebページのHTMLコーディングの機能を超えています。
ただし、重心からの体の最大距離がわかっている場合-アポプシス(アポヘリオン、太陽系惑星の場合)、ra –そしてそのような最小距離–近点(近日点)、rp –次に、軌道の離心率eは次のとおりです。
E =(ra – rp)/(ra+ rp)
軌道の離心率(UCAR)、地球の軌道の離心率(国立太陽観測所)、および時間の方程式(イリノイ大学)は、偏心度の高いWebサイトです。
離心率に関するSpace Magazineの記事?承知しました!例:自宅での月の離心率の測定、カイパーベルトオブジェクトのバフィー、タイタンでの湖の非対称性の説明。
離心率が重要な2つの天文学キャストエピソードは、海王星と地球です。よく聞く価値があります。